

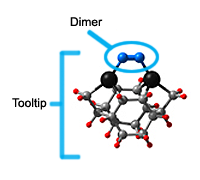
 |
Dimer tooltips - A dimer is a molecule made up of two similar, smaller molecules, or individual atoms, linked via a chemical bond. The dimer we are most interested in for this project is C2. A dimer tooltip is the business end of a much larger and stiffer molecular structure (the tool) composed of the dimer, and a structure that can both easily release the dimer onto a receptive surface, and be re-loaded with a new dimer.
Failure modes - A tooltip failure mode is when the tooltip structure morphs into some broken state. This could happen during the transfer of the dimer onto the receptive surface, during the re-loading of the tooltip, or even spontaneously due to thermal vibrations. A tooltip in failure mode can no longer engage in the transfer and deposition of dimers onto work surfaces. Tooltips with many failure modes are less desirable than those with few failure modes and that have high energy barriers to deformation. |
A tooltip in either normal or failure mode, has a structure with a minimum energy. The structure of a molecule stabilizes in these minimum energy states, ie, it takes additional energy to knock them out of these stable configurations. Searching for failure modes entails finding alternative minimum energy structures for a given tooltip molecule.
Another approach is to perform a molecular dynamics simulation of the molecule at a very high temperature so that the molecule deforms and undulates significantly, then perform quantum chemical geometry optimizations on each deformed variant produced in the simulation. This approach mechanizes the creation of initial, unstable structure variants that could then minimize to alternative structures.
This approach produces a large number of deforms to minimize via quantum chemistry software and would otherwise be too compute intensive if it were not for the NHAH computing network. The NHAH Quantum Search for Minimum Alternatives in Kinetically-Accessible Space (Q-SMAKAS) program creates work units (WUs) for the deforms that NHAH participants download and calculate with quantum chemistry software. The NHAH computing network has thousands of participants and can process all the deforms at once, making it very efficient in terms of time. The energies of the minimized structures sent back by the participants are compared with the minimum energies of the known alternative structures, and deltas exceeding a certain threshold flag possible newly discovered structures that are then reviewed manually and verified.
| Quantum Mechanics Engine | Sandia's MPQC program | Note: Since this geometry optimization is used only to find minimum energy deltas that are larger than 0.01 hartrees, RHF/3-21G is a sufficient level of theory. Candidate alternate structure verification optimizations are then performed at higher levels of theory such as B3LYP/6-31G(d,p). |
| Basis Set | 3-21G | |
| Method | Restricted Hartree-Fock | |
| Desired Optimization Convergence Criteria | Max gradient: 0.001 Max displacement: 0.001 | |
| Max Optimization Convergence Attempts | 40 | |
| Max Energy Convergence Attempts per Opt. Conv. Attempt | 100 |
 |
"The project all sounds well and good on paper, but doesn't mean anything without YOU (well, specifically, your computer(s), but no one will make that distinction in 10 years). Accordingly, there's no reason why you shouldn't have a broad and substantive understanding of what it is your machine is doing as related to this Q-SMAKAS project.
Every good project deserves a good explanation, so I'm going to attempt a thorough, albeit lighthearted, overview of this Q-SMAKAS project in 5 sections and hold myself to several hundred words a section (with the option to expand on contents with your (the reader's) further interest)."
Dr. Damian G. Allis |
| 1. | Allis, D. G. and Drexler, K. E. (2005). Design and Analysis of a Molecular Tool for Carbon Transfer in Mechanosynthesis. J. Comput. Theor. Nanosci. 2, 45-55. Free download here. |
| 2. | Freitas, R. A. Jr., Allis, D. G., and Merkle, R. C. (2007). Horizontal Ge-Substituted Polymantane-Based C2 Dimer Placement Tooltip Motifs for Diamond Mechanosynthesis. J. Comput. Theor. Nanosci. 4., 1-10. |