

| Biotin | |
| Heptane | |
| Octane |
Some of the larger tooltips took too long (several days) to converge with RHF/3-21G, so RHF/STO-3G was used instead. These lower levels of theory are both sufficiently accurate to detect failure modes (see Note on High Temperature/Low Level Logic.) The tooltips processed with RHF/STO-3G were: MCB5Ge, MCB57Ge, DCB75Ge, C100GeATD, C100GeATS, C100GeCTS, and MCB75Ge.
Using the optimized tooltip geometries, we then performed GROMACS molecular dynamics (MD) simulations on each of the tooltips at a high temperature for 50,000 iterations, taking snapshots of the tooltip every 40 or 50 iterations. The thermal energy of the high temperature simulations perturbed each tooltip wildly and the snapshots generated (kinetically accessible) tooltip deformations.
Initially, simulation at 1500 Kelvin was performed with each tooltip as a baseline level of tooltip deformation. The root mean square deviation (RMSD) of the tooltips at this temperature was around 0.02. An RHF/3-21G|STO-3G geometry optimization was then performed for each deformation on the NHAH network. No failure modes were discovered with this level of deformation.
Next, we performed simulations at a temperature yeilding an RMSD of at least 0.04 in 500 Kelvin steps. The range of temperatures used were: 2000 K, 2500 K, 3000 K, 3500 K, 4000 K, and 4500 K. An RHF/3-21G|STO-3G geometry optimization was then performed for each deformation on the NHAH network. Several potential failure modes were discovered at this level of deformation; they are under analysis.
The second column shows potential failure modes for the tooltip if any have been discovered so far. There is also a link to the mode's PDB file. The number and letter after the L/U indicates the deformed structure index and input dataset the mode came from. The mode's energy is also shown. If no potential failure modes have been discovered yet, the second column contains links to the input and output files (described below.)
The third column shows the number of initial deforms that minimized to the defect structure, a summary of the MD simulation performed to generate the initial deforms, and notes/observations about the defect. The MD simulation run summary line, eg, "MD run: 3500 K (0.04 RMSD)", shows the simulation environment temperature needed to produce tooltip deformations with the indicated RMSD.
The final row for each tooltip contains links to the input and results data files. The letter after the L/U indicates which simulation environment temperature was used to generate the tooltip deformations. The following table maps the letter to the temperature:
| z | 1500 K | y | 2000 K | x | 2500 K | w | 3000 K | v | 3500 K | u | 4000 K | t | 4500 K |
The low levels of theory (RHF/3-21G/STO-3G) are appropriate for these studies because this study is looking for strongly bound (covalent) tooltip structures. The strengths of covalent bonds are such that even low theory levels predict their connectivity correctly. The relative energies of these structures, however, will differ based on the level of theory. The generation of reasonable minimum energy candidate structures for the defect calculations requires more computational resources than the higher-level geometry optimizations of the identified defect structures because, for instance, 5000 defect starting structures taken from the GROMACS calculations may optimize to only 15 unique tooltip geometries, a consequence of not actively directing the generation of the defect structures.
2. Energy Units
The standard unit used in quantum chemistry for reporting the TOTAL ENERGY of molecules is the Hartree. The standard view in quantum chemistry is that a system of completely dissociated ("infinite separation") nuclei and electrons corresponds to zero energy (0 Hartree). This means the separation of a molecule into its component atoms AND the separation of each atom into its individual electrons and nucleus (the individual protons and neutrons in the nuclei are NOT included in this separation). As electrons and nuclei are brought closer to one another to form the molecule, the energy, as defined, decreases (more negative).
The only appropriate way to compare energies in quantum chemical calculations is to compare the SAME numbers of atoms at the SAME level of theory. Therefore, each tooltip and its defect structures are considered as distinct groups with no analysis overlap between different base tooltips (named structures).
There are two types of minimum energy structures considered in these (and all) calculations. The first is the GLOBAL minimum, the structure that yields to lowest possible energy for a given set of atoms at a given level of theory. The other type is the LOCAL minimum, a structure that is stable (as determined by performing quantum chemical vibrational analyses on the molecule) and will not spontaneously rearrange to a more stable form, but is higher in energy than the GLOBAL minimum (basically, all other stable forms). In theory (although part of the Q-SMAKAS project is to determine the validity of this statement), the "loaded" tooltip is the GLOBAL minimum energy form for these structures and each defect structure is a LOCAL minimum.
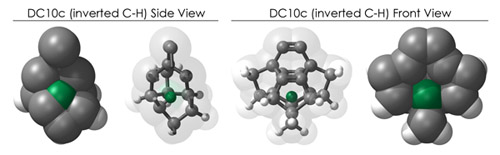
The "Look where it's going" reason - the most common hydrogen defect finds a C-H group on the outer surface of a tooltip inverting such that the C-H now points INTO the tooltip frame. One could imagine the surprise of reaching for your mouse with your right arm and instead firmly grasping your pancreas. While the tooltips are hollow structures, there is little-to-no room for stray hydrogen atoms.
Which brings up an important question. How do you get that crazy result in the first place?! In Q-SMAKAS, there are two reasons. The first reason is the easier of the two to understand. The temperature of the defect structure MD runs is hovering between 1500 and 4500 K. By comparison, room temperature is 300 K. These tooltips are being subjected to enormous energies, the result of which is the attainment of otherwise chemically inaccessible geometries.
The second reason is methodological. Molecular dynamics simulations require vectors and time steps. The vector is, of course, the momentum of the atom in question. The atoms will bounce around based on the energy of the system and the spring constants holding the atoms together. Simulation balances the energy of the system (wanting to move the atoms around) and the restoring forces of the bonds between atoms. In real life, the forces and motion "just are" and everything "just occurs." We can't calculate the instantaneous forces in the system and monitor it in "real time" because computers aren't yet fast enough. Instead, we perform the recalculations in the simulations at "time steps," intervals between which forces are allowed to do their thing bounded by instances when the system is recalculated to see where everything goes and where everything SHOULD go based on Netwon's Laws of motion.
Imagine driving down the highway - but you can only open your eyes for one second every five seconds. You open your eyes, correct your course, close your eyes and wait/hope, open again, correct, close, etc. If there's a curve in the road, or a barrier, you may over-shoot or under-shoot your course depending on how good your correction is. The situation in the molecular dynamics calculation is a further point complicated from this driving analogue. Because the simulator, and not the Earth, is responsible for all of the physics in the system, you and your car have no concept of what happens during those five second intervals of closed eyes, meaning you're just as likely to drive on a straight path as you would be through a brick wall. In the case of the simulator, since the wall isn't visible in those 5 seconds, you simply pass right through it. The same even CAN happen in the molecular dynamics simulation, where a sufficiently energetic hydrogen will simply "tunnel" through the nucleus of its attached carbon atom and come out the other side to form the new inverted geometry.
The dynamics simulator does not know that a hydrogen atom isn't allowed to pass through a carbon atom, it only knows that the hydrogen atom has a vector that says "go this far a second and await further instructions." Accordingly, a hydrogen can end up in some pretty unconventional positions if (a) the temperature is too high (huge vectors) or (b) the time step is too long (plenty of time move in a direction before the simulator stops it and recalculates the forces). This is a particular problem for the hydrogen because it is the lightest of the atoms, meaning it's also the one that moves around the most.
Our inverted hydrogen atoms, I suspect, are suffering more from the former, which means we could just back off on the time step. Alternatively, we can just increase the mass of the hydrogen atoms so that they don't move as freely as they seem to in the current runs. As our only goal is to find defects, there's nothing wrong with using a little magic in the simulator.
The "Hydrogen? What Hydrogen?" reason - the purpose of hydrogen in the universe is to satisfy unfilled valences in molecules. The goal of quantum chemical studies of dimer tooltips for diamondoid mechanosynthesis is to remove as much of the structure as possible so that the calculations (a) finish as quickly as possible and (b) can be run at as high a level of theory as possible to get the best results possible. The tooltips currently being studied are "bare minimum" structures that contain dimer, binding atoms (Ge or C), the nearest carbon atoms to the binding atoms to recreate the geometry of the binding atom/dimer complex, and hydrogen atoms everywhere an atom has a valence that needs filling. These tooltips, then, are bare minimum structures that run reasonable quickly on reasonable computers. In silico, the hydrogen atoms complete stable electron octets around the peripheral carbon atoms in the tooltip to keep the computational cost down. In reality (it is believed), these tooltips will be the leading edge of a complete tooltip assembly. That is, the hydrogen atoms causing the inverted defect forms simply won't be in the actual product and inverting a C-C group is, well, I don't want to be in the room when a factory full of it happens.
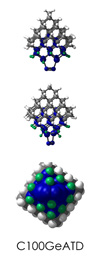
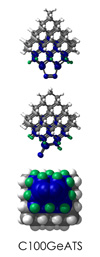
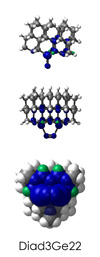
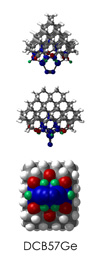
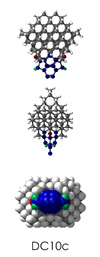
To demonstrate, I've put together some examples of extended tooltip-diamond frameworks in the images below (click to enlarge.) It is quite difficult for the hydrogen to invert when it isn't there. The process of embedding a tooltip into the diamond framework does remove many of the hydrogens in each of the tooltips (although there isn't a single tooltip that can be easily embedded that removes all of the hydrogen atoms in the immediate vicinity of the dimer binding position). The remaining hydrogen atoms in the images of the extended tooltips are shown in green around the blue core tooltip. It should not be assumed that these hydrogen atoms may be the ones to undergo inversion as found in the tooltip calculations. Inversion, as observed in the Q-SMAKAS runs, is an extremely high energy event and is most likely just a methodological artifact. It is, however, conceivable that these nearest hydrogen atoms may migrate on the tooltips under more mundane "defect" circumstances, a possibility that is part of the defect analysis. If this is found to be particularly easy for one tooltip or another, that clearly indicates that a particular tooltip may be too easily broken in a real manufacturing setting and should therefore be considered a possibly unusable structure.
It is worth noting/reminding that ALL of these tooltips are designed to do the same thing - bind and transfer carbon dimers. Accordingly, with a few caveats, the best one wins.
 |
 |
 |
 |
 |
 |
2.
 DC10c.L.pdb Mode: Normal Energy: -723.28856 Hartrees |
 DC10c.L.228v.pdb Mode: Hydrogen Inversion Energy: -723.13909 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0407 RMSD) using Deuterium 22 in MD run: 3500 K (0.0348 RMSD) 57 in MD run: 5500 K (0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||||||
 DC10c.L.563v.pdb Mode: Failure Energy: -723.16632 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0407 RMSD) using Deuterium 2 in MD run: 3500 K (0.0348 RMSD) 10 in MD run: 5500 K (0.04 RMSD) Notes: Tooltip base opened. The second defect (563) is a crack in the tooltip due to a hydrogen migration. This type of defect wouldn't otherwise occur in a Ge-based structure, as the double bond of the dimer binding section stabilizes the otherwise bare carbon. If more of the tool were present this may not happen? |
|||||||||||||||
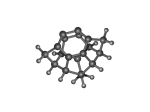 DC10c.L.719v.pdb Mode: Failure Energy: -723.28976 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3500 K (0.0348 RMSD) Notes: Failure mode (10) from the DC10c paper. RHF/3-21G puts this defect 3.15 kJ/mol more stable than the "normal" tooltip. This is one of those potentially problematic cases, as the nature of the defect is not one that's easily deflected by building out the tooltip structure (but there's a lot to be said for the barrier and the higher-level calculations.) |
|||||||||||||||
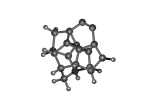 DC10c.L.928r.pdb Mode: Un-classified Energy: -723.17136 Hartrees |
Deforms that minimized to the alternate mode: 2 in MD run: 3000 K (0.0407 RMSD) using Deuterium 3 in MD run: 5500 K (0.04 RMSD) Notes: The four carbons opposite the dimer form two extra bonds. |
|||||||||||||||
| ||||||||||||||||
C100GeATD
 1_C100GeATD.L.pdb Mode: Normal Energy: -5280.93599 Hartrees |
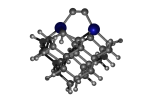 1_C100GeATD.L.929t.pdb Mode: Hydrogen Inversion Energy: -5280.68948 Hartrees |
Deforms that minimized to the alternate mode: 86 in MD run: 4500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms
Here are some "sleek" renderings of this tooltip mode courtesy of Andy Haveland-Robinson
Andy also rendered some ultra-cool videos of the 4500 Kelvin MD run: |
||||||||||
 1_C100GeATD.L.928t.pdb Mode: Thermally Inaccessible Energy: -5280.87534 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 4500 K (~0.04 RMSD) Notes: One hydrogen migrated to the dimer. The RHF/STO-3G energy difference from the "normal" tip is 159.51 kJ/mol and represents, by far, the lowest energy defect. Room temperature corresponds to about 2.5 kJ/mol, so we're talking about a defect high above thermal accessibility. |
|||||||||||
| ||||||||||||
C100GeATS
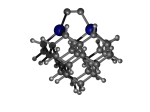 1_C100GeATS.L.pdb Mode: Normal Energy: -5280.98163 Hartrees |
 1_C100GeATS.L.647t.pdb Mode: Hydrogen Inversion Energy: -5280.50773 Hartrees |
Deforms that minimized to the alternate mode: 98 in MD run: 4500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
C100GeATSr5
 1_C100GeATSr5.L.pdb Mode: Normal Energy: -4705.93019 Hartrees |
 1_C100GeATSr5.L.609v.pdb Mode: Hydrogen Inversion Energy: -4705.72718 Hartrees |
Deforms that minimized to the alternate mode: 97 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
 1_C100GeATSr5.L.650v.pdb Mode: Un-classified Energy: -4705.82137 Hartrees |
Deforms that minimized to the alternate mode: 3 in MD run: 3500 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||||||
| ||||||||||||
C100GeATSr6
 1_C100GeATSr6.L.pdb Mode: Normal Energy: -4861.28173 Hartrees |
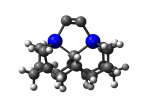 1_C100GeATSr6.L.424x.pdb Mode: Hydrogen Inversion Energy: -4861.18756 Hartrees |
Deforms that minimized to the alternate mode: 107 in MD run: 2500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
C100GeCTS
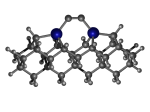 1_C100GeCTS.L.pdb Mode: Normal Energy: -5283.35665 Hartrees |
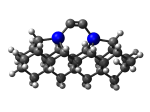 1_C100GeCTS.L.123v.pdb Mode: Hydrogen Inversion Energy: -5283.11688 Hartrees |
Deforms that minimized to the alternate mode: 26 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||
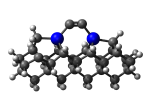 1_C100GeCTS.L.511v.pdb Mode: Un-classified Energy: -5283.17814 Hartrees |
Deforms that minimized to the alternate mode: 4 in MD run: 3500 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||
| ||||||||
C110GeS
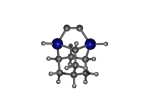 2_C110GeS.L.pdb Mode: Normal Energy: -4515.37009 Hartrees |
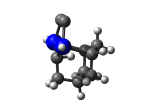 2_C110GeS.L.424v.pdb Mode: Hydrogen Inversion Energy: -4515.23658 Hartrees |
Deforms that minimized to the alternate mode: 102 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
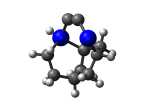 2_C110GeS.L.558v.pdb Mode: Un-classified Energy: -4515.36179 Hartrees |
Deforms that minimized to the alternate mode: 2 in MD run: 3500 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||||||
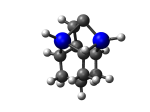 2_C110GeS.L.783v.pdb Mode: Un-classified Energy: -4515.32278 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3500 K (~0.04 RMSD) Notes: Dimer is held by just one carbon with the other carbon bound back onto the tooltip; and a hydrogen migrated to the dimer. |
|||||||||||
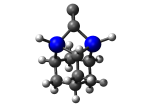 2_C110GeS.L.613v.pdb Mode: Un-classified Energy: -4515.37451 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3500 K (~0.04 RMSD) Notes: Dimer is held by just one carbon with the other carbon protruding from the tooltip; lower energy mode. |
|||||||||||
| ||||||||||||
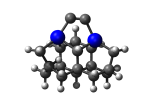
C111Ge3
 3_C111Ge3.L.pdb Mode: Normal Energy: -4821.32074 Hartrees |
 3_C111Ge3.L.814v.pdb Mode: Hydrogen Inversion Energy: -4821.18351 Hartrees |
Deforms that minimized to the alternate mode: 84 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
AdamGe22
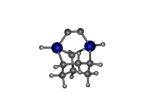 5_AdamGe22.L.pdb Mode: Normal Energy: -4476.53808 Hartrees |
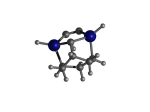 5_AdamGe22.L.23v.pdb Mode: Hydrogen Inversion Energy: -4476.38819 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0402 RMSD) using Deuterium 6 in MD run: 3500 K (0.0413 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||||||
 5_AdamGe22.L.208v.pdb Mode: Failure Energy: -4476.53628 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0402 RMSD) using Deuterium 1 in MD run: 3500 K (0.0413 RMSD) Notes: Strange dimer orientation. A subtle structural change, with the arrangement of the dimer on the Ge...Ge displaced from its preferred arrangement, which is only 4.7 kJ/mol lower (so we're looking at wobble in the dimer.) |
|||||||||||||||
 5_AdamGe22.L.787v.pdb Mode: Failure Energy: -4476.52428 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0402 RMSD) using Deuterium 1 in MD run: 3500 K (0.0413 RMSD) Notes: Tooltip opened up. A hydrogen migration from a Ge atom onto the nearest C atom that the Ge was attached to. The Ge-C bond is broken with this. |
|||||||||||||||
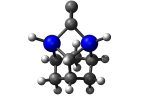 5_AdamGe22.L.701w.pdb Mode: Failure Energy: -4476.54660 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (0.0402 RMSD) using Deuterium Notes: Dimer is held by just one carbon with the other carbon protruding from the tooltip. Lower energy configuration. |
|||||||||||||||
| ||||||||||||||||
AdamGe33
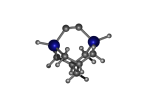 5_AdamGe33.L.pdb Mode: "Normal" Energy: -4477.73819 Hartrees |
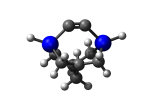 5_AdamGe33.L.275w.pdb Mode: Hydrogen Inversion Energy: -4477.66301 Hartrees |
Deforms that minimized to the alternate mode: 93 in MD run: 3000 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
 5_AdamGe33.L.568w.pdb Mode: Un-classified Energy: -4477.70575 Hartrees |
Deforms that minimized to the alternate mode: 2 in MD run: 3000 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||||||
| ||||||||||||
Diad3Ge22
 6_Diad3Ge22.L.pdb Mode: Normal Energy: -4783.59967 Hartrees |
 6_Diad3Ge22.L.911x.pdb Mode: Hydrogen Inversion Energy: -4783.42440 Hartrees |
Deforms that minimized to the alternate mode: 3 in MD run: 2500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
 6_Diad3Ge22.L.152x.pdb Mode: Failure Energy: -4783.59967 Hartrees |
Deforms that minimized to the alternate mode: ?? in MD run: 2500 K (0.04 RMSD) Notes: Dimer changed sides. Detected via visual inspection of the MD run - otherwise it has the same energy as the normal mode tooltip. Counting them would be a pain because we'd have to do it manually/visually since energy gives no indication. Come up with an algorithm to automatically detect symmetric deformations by labeling a select triple/triangle of atoms, then do a fuzzy comparison to atoms in the immediate vicinity of the binding pocket. |
|
 6_Diad3Ge22.L.156x.pdb Mode: Failure Energy: -4783.55711 Hartrees |
Deforms that minimized to the alternate mode: 13 in MD run: 2500 K (0.04 RMSD) Notes: Dimer twisted. One class of interesting defect here, resulting from the flip of one of the H atoms on the Ge...Ge region (so the H's aren't both on the same side anymore). The flipped case is 111 kJ/mol higher than the "normal" tooltip. |
|
DCB55AGe
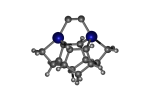 7_DCB55AGe.L.pdb Mode: Normal Energy: -4743.61394 Hartrees |
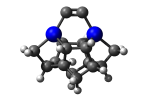 7_DCB55AGe.L.953t.pdb Mode: Hydrogen Inversion Energy: -4743.54031 Hartrees |
Deforms that minimized to the alternate mode: 121 in MD run: 4500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCB55BGe
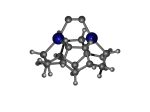 7_DCB55BGe.L.pdb Mode: Normal Energy: -4821.21100 Hartrees |
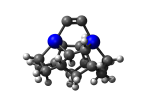 7_DCB55BGe.L.432w.pdb Mode: Hydrogen Inversion Energy: -4743.54031 Hartrees |
Deforms that minimized to the alternate mode: 20 in MD run: 3000 K (0.0610 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCB55CGe
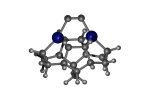 7_DCB55CGe.L.pdb Mode: Normal Energy: -4858.87444 Hartrees |
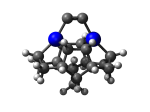 7_DCB55CGe.L.398v.pdb Mode: Hydrogen Inversion Energy: -4858.84148 Hartrees |
Deforms that minimized to the alternate mode: 125 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCB57Ge
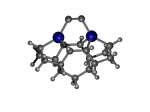 7_DCB57Ge.L.pdb Mode: Normal Energy: -4858.94184 Hartrees |
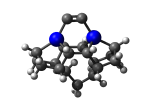 7_DCB57Ge.L.573u.pdb Mode: Hydrogen Inversion Energy: -4858.85935 Hartrees |
Deforms that minimized to the alternate mode: 132 in MD run: 4000 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
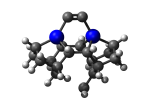 7_DCB57Ge.L.302u.pdb Mode: Un-classified Energy: -4858.76556 Hartrees |
Deforms that minimized to the alternate mode: 2 in MD run: 4000 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||||||
| ||||||||||||
DCB5Ge
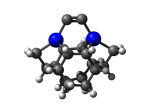 7_DCB5Ge.L.pdb Mode: Normal Energy: -4821.22754 Hartrees |
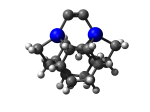 7_DCB5Ge.L.445w.pdb Mode: Hydrogen Inversion Energy: -4821.17042 Hartrees |
Deforms that minimized to the alternate mode: 46 in MD run: 3000 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
 7_DCB5Ge.L.111w.pdb Mode: Un-classified Energy: -4821.17948 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 3000 K (~0.04 RMSD) Notes: Dimer cracked. |
|||||||||||
| ||||||||||||
DCB65Ge
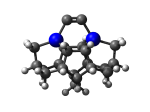 7_DCB65Ge.L.pdb Mode: Normal Energy: -4936.57467 Hartrees |
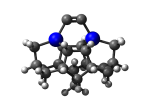 7_DCB65Ge.L.320w.pdb Mode: Hydrogen Inversion Energy: -4936.54164 Hartrees |
Deforms that minimized to the alternate mode: 192 in MD run: 3000 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCB6Ge
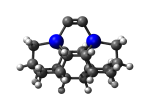 7_DCB6Ge.L.pdb Mode: Normal Energy: -4897.82372 Hartrees |
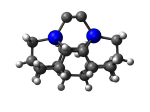 7_DCB6Ge.L.711v.pdb Mode: Hydrogen Inversion Energy: -4897.70150 Hartrees |
Deforms that minimized to the alternate mode: 90 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCB75Ge
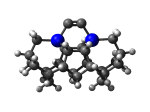 7_DCB75Ge.L.pdb Mode: Normal Energy: -5096.09096 Hartrees |
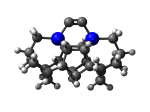 7_DCB75Ge.L.274x.pdb Mode: Hydrogen Inversion Energy: -5096.03682 Hartrees |
Deforms that minimized to the alternate mode: 478 in MD run: 2500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
DCBIceane7Ge
 7_DCBIceane7Ge.L.pdb Mode: Normal Energy: -4630.64599 Hartrees |
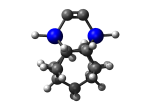 7_DCBIceane7Ge.L.721v.pdb Mode: Hydrogen Inversion Energy: -4630.55822 Hartrees |
Deforms that minimized to the alternate mode: 31 in MD run: 3500 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
| ||||||||||||
MCB55Ge
 7_MCB55Ge.L.pdb Mode: Normal Energy: -4860.03772 Hartrees |
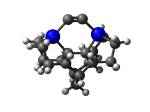 7_MCB55Ge.L.373q.pdb Mode: Hydrogen Inversion Energy: -4860.08270 Hartrees |
Deforms that minimized to the alternate mode: 10 in MD run: 6000 K (~0.08 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
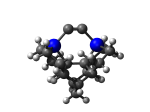 7_MCB55Ge.L.800q.pdb Mode: Un-classified Energy: -4860.13980 Hartrees |
Deforms that minimized to the alternate mode: 3 in MD run: 6000 K (~0.08 RMSD) Notes: Hydrogen re-arrangement to significantly lower energy - suggests a new, more stable tooltip? |
|||||||||||
| ||||||||||||
MCB57Ge
 7_MCB57Ge.L.pdb Mode: Normal Energy: -5020.12499 Hartrees |
No alternate modes detected. | |||||||||||
| ||||||||||||
MCB5Ge
 7_MCB5Ge.L.pdb Mode: Normal Energy: -4942.96584 Hartrees |
No alternate modes detected. | |||||||||||
| ||||||||||||
MCB75Ge
 7_MCB75Ge.L.pdb Mode: Normal Energy: -5361.42659 Hartrees |
No alternate modes detected. | |||||||
| ||||||||
TwistaneGe
 9_TwistaneGe.L.pdb Mode: Normal Energy: -4438.88518 Hartrees |
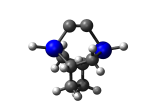 9_TwistaneGe.L.701u.pdb Mode: Hydrogen Inversion Energy: -4438.73775 Hartrees |
Deforms that minimized to the alternate mode: 24 in MD run: 4000 K (~0.04 RMSD) Notes: One or more hydrogens inverted to inside the tooltip. Ignorable - see The "Catalytic Handwaving" of Inverted Hydrogen Atoms |
||||||||||
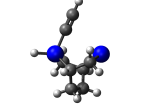 9_TwistaneGe.L.238u.pdb Mode: Un-classified Energy: -4438.90750 Hartrees |
Deforms that minimized to the alternate mode: 1 in MD run: 4000 K (~0.04 RMSD) Notes: Dimer is held by just one carbon with the other carbon protruding from the tooltip and with a hydrogen attached. Lower energy configuration. |
|||||||||||
| ||||||||||||